↜ Back to index Introduction to Numerical Analysis 1
Part a—Lecture 7
In today’s lecture we change the topic slightly and talk about solving nonlinear algebraic equations numerically. Next week we use this knowledge to help us solve ODEs.
Consider the equation F(x) = 0 for given function F: {\mathbb{R}}\to {\mathbb{R}} is a given function. We are interested in approximating a solution x \in {\mathbb{R}} of this equation, also called a zero or root of F, numerically.
Example 1. Any equation can be converted into the above form with an appropriate F. For example, for the equation \cos x = \exp x + 2 we can take F(x) := \cos x - \exp x - 2 or F(x) := \exp x + 2 - \cos x, or even F(x) = \frac 1{\cos x - \exp x -1} - 1 (but we need to be a bit careful about the domain of this function).
Simple equations like 2 x - 3 = 0 and x^2 + 4 = 0 have a formula that gives a solution explicitly. Note that the latter equation has only complex solutions.
In general, there might be no formula for a solution of a given equation or the formula is using functions that are difficult to evaluate.
Example 2. A transcendental equation \exp x + x = 0 has a solution x = - W(1) \approx -0.567143 according to Wolfram Alpha. Here W is the product log function. How do we compute W(1)? Well, it’s not easy.
For equation \cos x = x\qquad (F(x) = \cos x - x \text{ for example}) Wolfram Alpha only gives an approximate numerical value.
Cubic equations like x^3 - x - 1 = 0 can be solved using various formulas (see the solution on Wolfram Alpha), but the formulas are very complicated in general.
Newton’s method
Newton's method or Newton-Raphson method is one of the commonly used numerical methods for finding a solution of nonlinear equations F(x) = 0 (finding a root of F) when F is a differentiable function.
The main idea is to start with x_0 \in {\mathbb{R}} near an actual zero of F, and then approximate F by its first-order Taylor polynomial around x_0: F(x) \approx F(x_0) + F'(x_0) (x - x_0). We can easily find the solution of the linear equation F(x_0) + F'(x_0) (x - x_0) = 0 as x_1 = x_0 -\frac{F(x_0)}{F'(x_0)}, provided that F'(x_0) \neq 0.
We then proceed iteratively by doing the Taylor series at x_1, finding the solution x_2 of the linearized equation, in general, x_{k+1} = x_k - \frac{F(x_k)}{F'(x_k)}, \qquad k = 0, 1, 2, \ldots. If the function F has a nonzero derivative at the actual root and our choice of x_0 was “good”, the sequence x_n will converge to the actual root very quickly. In fact, in general the number of correct decimal digits will double in each iteration.
Example 3. Consider the quadratic equation x^2 - 1 = 0. It is clear that the equation has 2 roots, x = 1 and x = -1. Let us use Newton’s method to find one of these roots.
We can take F(x) = x^2 - 1 and F'(x) = 2x. Therefore the iterative formula for Newton’s method is
x_{k+1} = x_k - \frac{x_k^2 - 1}{2x_k}
Here is a sample code in Fortran. We do 5 iterations of the Newton’s method.
! Implementation of Newton's method for x^2 - 1 = 0
implicit none
real x, F, Fprime
integer i
! Enter the starting x0
read *, x
print *, x
do i = 1, 5
! To solve a different equation, we just need to modify these formulas
F = x**2 - 1
Fprime = 2 * x
! Fprime cannot be zero (or too small, there might be a problem)
if (abs(Fprime) < 1e-6) then
print *, 'Error: the derivative is too close to zero'
stop
endif
x = x - F / Fprime
print *, x
enddo
endWith initial guess 2, the method converges to the exact solution very fast:
$ ./a.exe <<< 2
2.00000000
1.25000000
1.02499998
1.00030482
1.00000000
1.00000000 You can see that the number of correct digits approximately doubles in each iteration.
What if we start close to 0?
$ ./a.exe <<< 0.001
1.00000005E-03
500.000488
250.001251
125.002625
62.5053101
31.2606544 In this case we first go very far from the correct solution and then converge relatively slowly. Do you see why?
It is therefore very important to choose a good starting point.
For a negative starting value, we end up at -1:
$ ./a.exe <<< -0.5
-0.500000000
-1.25000000
-1.02499998
-1.00030482
-1.00000000
-1.00000000 And if we choose wrong, we get an error:
$ ./a.exe <<< 0
0.00000000
Error: the derivative is too close to zeroAssuming that the x_k converges to the root 1, let us see how the error {\varepsilon}_k := |x_k - 1| of the method behaves. First we subtract 1 from both sides of Newton’s method formula: x_{k+1} - 1 = x_k - 1 - \frac{x_k^2 - 1}{2x_k} and using x_k^2 - 1 = (x_k - 1)(x_k + 1) we get x_{k+1} - 1 = (x_k - 1)\left(1 - \frac{x_k + 1}{2x_k}\right) = (x_k-1)\frac{2x_k - x_k - 1}{2x_k} = \frac{(x_k - 1)^2}{2x_k}. Taking the absolute value of both sides, we have {\varepsilon}_{k+1} = \frac 1{2|x_k|} {\varepsilon}_k^2. So if we take x_0 \in (0.5, 1.5), we see that {\varepsilon}_{k+1} \leq {\varepsilon}_k^2 and the number of zeros after the decimal point of {\varepsilon}_k at least doubles in each iteration.
Example 4. For a \neq 0, consider the equation ax = 1. The solution is obviously x = 1/a, but let us see what we get from Newton’s method for a specific choice of F.
Taking F(x) = \frac 1x - a, we have F'(x) = -\frac 1{x^2} and so Newton’s method iteration reads x_{k+1} = x_k - \frac{\frac 1{x_k} - a}{-\frac 1{x_k^2}} = 2x_k - ax_k^2. There are no divisions in the formula. We can compute 1/a using only subtraction and multiplication. This is sometimes quite useful. Unfortunately, the initial guess x_0 needs to be quite good for fast convergence.
A summary of features of Newton’s method:
It is not robust: convergence to a root depends on the choice of the initial guess x_0. We have to make sure to choose a good x_0. For more details see failure analysis. We might have to use another more robust method like the bisection method to find a good initial guess.
If it converges, the convergence is usually very fast: each iteration approximately doubles the number of valid decimal digits in the solution.
It can only be applied to equations F(x) = 0 if F is differentiable.
It is best used if the formula for F' can be easily evaluated.
When using Newton’s method, we usually do not know how many iterations we need to get a solution with certain accuracy. Therefore it is useful to add a stopping condition that uses |x_{k+1} - x_k| as an estimate on the error of the solution and stops when it is smaller than a certain value, that is, when |x_{k+1} - x_k| < tol for some chosen tol, for example tol = 10^{-3}. If we use this stopping condition, We can expect that the error of x_{k+1} is about tol^2.
! Implementation of Newton's method for x^2 - 1 = 0
! with a stopping condition
implicit none
real x, F, Fprime, d
integer k
! Enter the starting x0
read *, x
do k = 1, 100
F = x**2 - 1
Fprime = 2 * x
if (abs(Fprime) < 1e-6) then
print *, 'Error: the derivative is too close to zero'
stop
endif
d = F / Fprime
x = x - d
! We stop the iteration if x does not change more than a certain value
if (abs(d) < 1e-3) then
print *, k, 'iterations needed'
! stop the loop
exit
endif
enddo
print *, 'x =', x
endHere are a few examples of running the above code with different x_0:
$ ./a.exe <<< 1
1 iterations needed
x = 1.00000000 $ ./a.exe <<< 2
4 iterations needed
x = 1.00000000 $ ./a.exe <<< 0.0001
17 iterations needed
x = 1.00000000 $ ./a.exe <<< -0.5
4 iterations needed
x = -1.00000000 Exercises
Exercise 1. Use Newton’s method to find a solution of the equation
\exp(x) + x = 5
Use stopping tolerance tol = 10^{-3} for |x_{k+1} - x_k|. Report the number of iterations needed to reach this tolerance for x_0 = -100, x_0 = 0 and x_0 = 10.
Exercise 2.
Use Newton’s method to solve the cubic equation x^3 + px + q = 0 where p, q \in {\mathbb{R}} are given. Use stopping tolerance tol = 10^{-3}. The program should read p, q and x_0 from the keyboard and print the approximate solution after the stopping tolerance is reached. If the stopping tolerance is not reached in 100 iterations, the program should print a message that the method does not converge.
Example. With p = -2, q = -5 and x_0 = 5, this is a possible output:
$ ./a.exe <<< "-2 -5 5"
5.00000000
3.49315071
2.60783577
2.19920921
2.10023665
2.09456968
x = 2.09455156
6 iterations neededTest the program with p = -2 and q = 2.
For which of the following initial guesses does the program converge to the exact solution -1.7693\ldots? Can you explain the behavior by looking at the graph of x^3 -2p + 2?
x_0 = -2
x_0 = 0
x_0 = 10
x_0 = 100
Test the program with p = q = 0 and x_0 = 1.
How many iterations do you need to reach convergence?
Is the error of the obtained solution within tol^2 = 10^{-6} of the correct solution 0 as usually?
(Explanation: Since the x^3 = 0 has a triple root at 0, Newton’s method converges much slower than usually and the error in the root is much bigger than we would expect from the stopping condition. We have to be careful with such degenerate roots. Usually you want to have F' \neq 0 at the root so that the linear approximation makes sense near the root.)
Exercise 3.
With fixed p = -2, q = 2, modify the program in the previous exercise to do the following: The program should read a positive integer r from the keyboard and then for each x_0 = -r, -r + 1, \ldots, r it should print the number of iterations Newton’s method needs to converge to the solution with tol = 10^{-3}. If the method does not converge within 100 iterations, the program should not print anything for such x_0.
This is how the output should look like for r = 5:
$ ./a.exe <<< 5 -5 6 -4 6 -3 5 -2 3 -1 7 2 8 3 18 4 17 5 18Note that the output for 0 and 1 is missing since with these x_0 Newton’s method does not converge to the solution.
Submit the code to LMS.
Run the program with r = 1000 and plot the data using gnuplot with x_0 on the horizontal axis and the number of iterations on the vertical axis.
Submit the plot to LMS with your student ID number as the title.
Example. This is how the plot looks for r = 10:
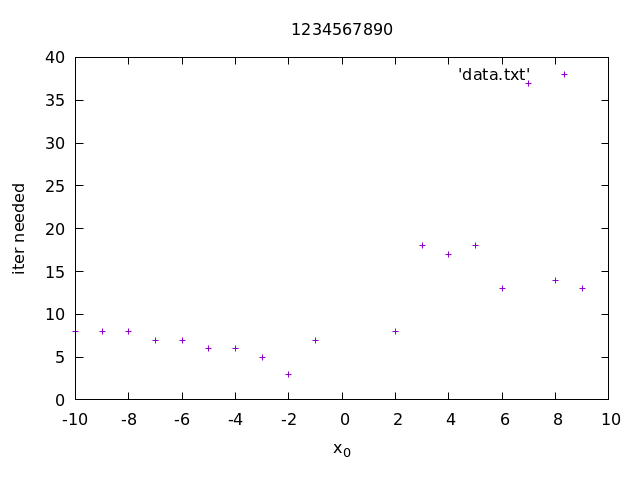
For r = 1000 you should see an interesting pattern for x_0 > 0. For more explanation and fun ideas, see Newton fractal on Wikipedia.